拳交 av 8000字详解“降维算法”,从表面罢了到案例阐发 | 东谈主东谈主齐是居品司理

无监督学习中的两种算法,之前咱们共享了聚类算法,本文来先容着落维算法。从倡导开头拳交 av,了解当时期旨趣和特色后谄媚场景案例,加深咱们对降维算法的应用和表露。
其实降维算法没那么复杂,是无监督学习的一种应用,粗略来说就是:握重心。

迎接一谈探索AI的天下。
无监督学习中比拟常见的有两类算法,一个是聚类算法,还有一个是降维算法。
对于聚类算法,我在上一篇《8000字详解“聚类算法”,从表面罢了到案例阐发》中有重心说到,先容了聚类算法中的K均值聚类算法和档次聚类算法。从基本倡导提及,聊到算法罢了的枢纽,通过假定案例带入实质场景。
比如,K均值聚类算法不错将客户分为不同的群体,能匡助企业更好地了解客户,制定更有用的营销政策。
档次聚类算法中的AGNES算法不错将同样的文档归为一类,匡助企业更好地料理和分析文档。DIANA算法不错完成学情分析,匡助学校或训诫机构更好地了解学生的学习情况,制定更有用的训诲政策。
本篇,咱们一谈来学习了解降维算法,先从倡导处开头,平缓了解当时期旨趣和特色,终末再谄媚场景案例,加深咱们对降维算法的应用和表露。
全文8000字左右,预测阅读时分15分钟,如果碎屑时分不够,提倡先保藏后看,便于找回。
照例,开篇提供本篇著作的目次大纲,精真金不怕火全球在阅读前统领全局,对内容框架有事前了解。

降维算法是机器学习顶用于减少数据集维度的一种时期,其想法是在尽可能保留数据中有用信息的前提下,裁减数据的复杂性。
减少数据集维度是指通过数学变换或特征弃取等方法,裁减数据聚合特征的数目或裁减数据点在某个空间中的示意的维度。这一过程常常被称为降维(Dimensionality Reduction)。
减少数据集维度的主要想法是为了简化数据模子,提高数据处理的成果,并可能改善模子的性能。
在实质应用中,数据集时常包含多数的特征,这些特征中有的可能彼此相关,有的可能是噪声或冗余的。如果平直在这些特征上构建模子,可能会导致模子复杂度高,训练时分长,且容易过拟合。
正因为如斯,咱们需要降维算法出马,来减少数据集维度,贬责各式实质问题。
1. 降维的三大上风在说降维算法之前,咱们先单独聊聊降维,降维有三大上风:去除冗余特征、裁减野心复杂度、利于数据可视化。
上风一:【去除冗余特征】
在数据中,一些特征可能是其他特征的线性组合,或者与某些特征高度相关。冗余特征不仅会加多模子的复杂性,还可能导致过拟合,裁减模子的泛化能力。通过降维,咱们不错去除这些冗余特征,从而简化模子。
假定咱们有一个对于房价的数据集,其中包含了房屋的大小(Feature A)、房屋的年级(Feature B)、房屋的卧室数目(Feature C)和房屋的卫生间数目(Feature D)。
如果咱们发现Feature A和Feature B之间存在高度相关性(例如,房屋年级越大,常常房屋面积也越大),那么Feature A就不错被Feature B所线性示意。
在这种情况下,咱们不错沟通去除Feature A,因为它提供了与Feature B同样的信息。
又例如,如果咱们发现Feature C和Feature D之间也存在高度相关性,这可能意味着卧室数目和卫生间数目在某种进度上是相关的(例如,在一些地区,跟着房屋面积的加多,卧室和卫生间数目也会加多)。
在这种情况下,咱们不错沟通去除其中一个特征,因为它们可能包含冗余信息。
从例子中,咱们通畴昔除一些冗余特征,就不错简化模子,裁减模子的复杂性,并可能提高模子的性能。
不外在实质应用中,弃取合适的特征去除方法需要字据数据的特色和业务需求来决定,切不能无脑照搬。
上风二:【裁减野心复杂度】
裁减野心复杂度是降维不错贬责的另一大问题,尤其是在处理大限制数据集时。通过减少数据集的维度,不错权贵减少模子所需的野心资源,从而加速训练和预测的速率。
假定咱们有一个对于用户行为的数据集,其中包含了千千万万个特征,如用户的东谈主口统计信息、浏览历史、购买记载等。
如果平直在这些特征上构建一个线性总结模子,模子可能会相当复杂,训练和预测的速率会很慢。
关联词通过使用主因素分析(PCA)进行降维,咱们不错将原始特征的数目减少到几百个最焦躁的特征,这些特征巧合讲明大部分的方差。
在这种情况下,降维后的模子将具有更少的参数,训练和预测的速率将权贵提高。其中,主因素分析(PCA)是降维算法中比拟常见的算法之一,咱们后续会西宾到。
香港三级电影上风三:【利于数据可视化】
降维还不错匡助咱们更好地表露和可视化数据,通过将高维数据投影到二维或三维空间,咱们不错更容易地细察数据的结构和形状。
高维数据投影到二维或三维空间后,咱们不错使用各式可视化器具来辅助分析,如散点图、柱状图、热力求等,来展示数据之间的关系和形状。
假定咱们有一个对于酬酢汇集用户的数据集,其中包含了用户的基本信息(如年级、性别、地舆位置等)以及他们的酬酢行为(如发帖频率、互动数目、内容类型等)。这个数据集可能是高维的,包含了成百上千个特征。
为了更好地表露这个酬酢汇集的数据结构和用户群体的行为形状,咱们不错使用降维时期来简化数据。
例如,咱们不错使用主因素分析(PCA)将数据投影到二维空间,然后使用t-SNE进一步细化到低维空间。
t-SNE是一种基于概率的降维时期,它巧合在低维空间中保持高维空间中数据点之间的同样性。t-SNE常常用于生成数据点之间的复杂关系图,从而更好地表露数据的结构。
通过以上的降维处理,咱们不错生成一张二维的散点图,每个点代表一个用户,点的坐标由PCA或t-SNE算法笃定。
在这个散点图中,咱们不错细察到不同庚级、性别和地舆位置的用户的酬酢行为形状。
例如,咱们不错看到哪些类型的用户更活跃,哪些类型的用户更倾向于与特定类型的内容互动。
通过这么的数据可视化,咱们不错直瞻念地看到用户群体的散布和行为形状,它不错匡助咱们识别想法用户群体,了解他们的行为风俗,并据此优化用户体验,提高用户参与度和餍足度。

既然降维有那么多公正,那么它又是如安在东谈主工智能边界发达其上风的呢?这源于降维的两大方法:特征弃取和特征索要。
方法一:【特征弃取】
特征弃取是从原始特征聚合中弃取出一组对想法变量有较强讲明能力的特征子集的过程。这一过程的想法是去除冗余特征和不相关的特征,以简化模子并提高模子的性能。特征弃取不蜕变数据自己的维度,仅仅简化特征空间。
比如,基于相关性分析来罢了特征弃取,通过野心特征与想法变量之间的相关统共或相关性矩阵,不错找出与想法变量相关性较高的特征。
常常弃取相关性较高的特征,去除相关性较低的特征。因为相关性较高的特征常常被合计对想法变量有较强的讲明能力,而相关性较低的特征可能与想法变量关系不大或包含冗余信息。
就拿咱们刚例如过的房价数据集来链接假定一下吧。
房价的数据聚合包含了房屋的大小(Feature A)、房屋的年级(Feature B)、房屋的卧室数目(Feature C)和房屋的卫生间数目(Feature D),咱们的想法是预测房价。
通过相关性分析,咱们野心了每个特征与房价之间的相关统共。假定咱们发现Feature A(房屋的大小)与房价之间的相关统共为0.8,而Feature B(房屋的年级)与房价之间的相关统共为0.5。
在这种情况下,咱们不错合计Feature A与房价之间的关联进度更高,因此弃取Feature A行动焦躁的特征。而Feature B与房价之间的关联进度较低,可能包含冗余信息或其他不焦躁的因素。
因此,咱们可能会沟通去除Feature B,或者在模子中给以较低的权重。这即是降维中的特征弃取方法在实质问题中不错应用的所在。
方法二:【特征索要】拳交 av
特征索要是通过数学变换将高维数据映射到低维空间的过程,同期尽可能保留原始数据中的信息,这种方法会蜕变数据的维度。特征索要的想法是减少数据的复杂性,同期保持数据的主要结构和特征。
由表面代入延迟,咱们来链接假定一些案例。
假定咱们有一个对于酬酢媒体平台用户生成内容的数据集,其中包含了用户的帖子、研究、点赞、共享等互动行为,以及用户的东谈主口统计信息、地舆位置、有趣偏好等特征。
咱们期许通过数据集分析用户行为形状,识别有影响力的内容创作家,以及发现热点话题。
为了简化这个高维数据集并识别出枢纽的用户行为和内容特征,咱们不错使用主因素分析(PCA)进行特征索要。
通过PCA,咱们不错将原始数据投影到二维空间,生成一张散点图。在这个散点图中,咱们不错细察到不同用户或内容的互动形状,以及它们如何与特定的东谈主口统计特征或有趣偏好相关联。
又或者,在文本数据分析中,每条帖子或研究齐不错被示意为一个高维的特征向量,包括词汇频率、情谊分析得分、主题模子等。
通过使用PCA或t-SNE进行特征索要,咱们不错将文本的特征向量裁减到二维或三维,生成一张关系图。
在这个关系图中,咱们不错细察到内容之间的同样性和互异性,从而更好地表露内容的主题散布和用户互动形状。
通过这么的特征索要,咱们不错识别出对用户行为和内容趋势最焦躁的特征,如情谊倾向、话题相关性、互动热度等,从而简化数据并保持数据的主要结构和特征。
这对于新媒体平台的内容政策制定、用户参与度援助和市集趋势分析相当焦躁,因为它不错匡助他们优化保举算法,援助用户体验,并制定更有用的内容营销政策。
通过特征索要,通过数学变换将高维数据映射到低维空间,简化数据并保持数据的主要结构和特征,不错在好多业务场景中发达算法的魔力。

如果说,降维是一个想法,那么降维算法就是达到想法的具体时期或方法。降维是通过减少数据集的维度来简化数据的过程,而降维算法规是通过数学变换或特征弃取,将这过程得以罢了。
在东谈主工智能边界,咱们常用的降维算法有主因素分析(PCA)、线性判别分析(LDA)、因子分析(Factor Analysis)、局部线性镶嵌(LLE)、等距映射(Isomap)、t-SNE、自编码器(Autoencoder)等。
主因素分析(PCA)
旨趣:PCA通过正交变换将数据投影到新的坐标系上,使得新坐标系的前几个主因素巧合讲明大部分的方差。
应用:PCA常用于数据可视化、特征索要和噪声过滤。
线性判别分析(LDA)
旨趣:LDA旨在找到投影标的,使得不同类别的样本尽可能分开,而同类的样本尽可能聚合。
应用:LDA常用于特征弃取和分类任务,特等是在需要沟通不同类别间互异的情况下。
因子分析(Factor Analysis)
旨趣:因子分析肖似于PCA,但它试图找到数据的潜在因子结构,并允许因子之间存在相关性。
应用:因子分析常用于心思学、市集磋磨等边界,用于发现数据中的潜在维度。
局部线性镶嵌(LLE)
旨趣:LLE是一种非线性降维方法,它试图保持数据在低维空间中的左近性关系。
应用:LLE适用于发现非线性数据中的结构,常用于图像和文本数据的降维。
等距映射(Isomap)
旨趣:Isomap是一种基于流形的降维时期,它通过保持数据点之间的局部距离关系来裁减数据的维度。
应用:Isomap适用于高维空间中的数据,特等是在数据点之间存在复杂非线性关系时。
t-SNE
旨趣:t-SNE是一种基于概率的降维时期,它试图在低维空间中保持高维空间中数据点之间的同样性。
应用:t-SNE常用于生成数据点之间的复杂关系图,从而更好地表露数据的结构,特等是在图像和文本数据中。
自编码器(Autoencoder)
旨趣:自编码器是一种神经汇集,它试图通过编码器将数据编码到一个低维空间,然后通过解码器重建原始数据。
应用:自编码器不错用于无监督的降维,特等是在数据量较大时,也常用于特征学习和数据去噪
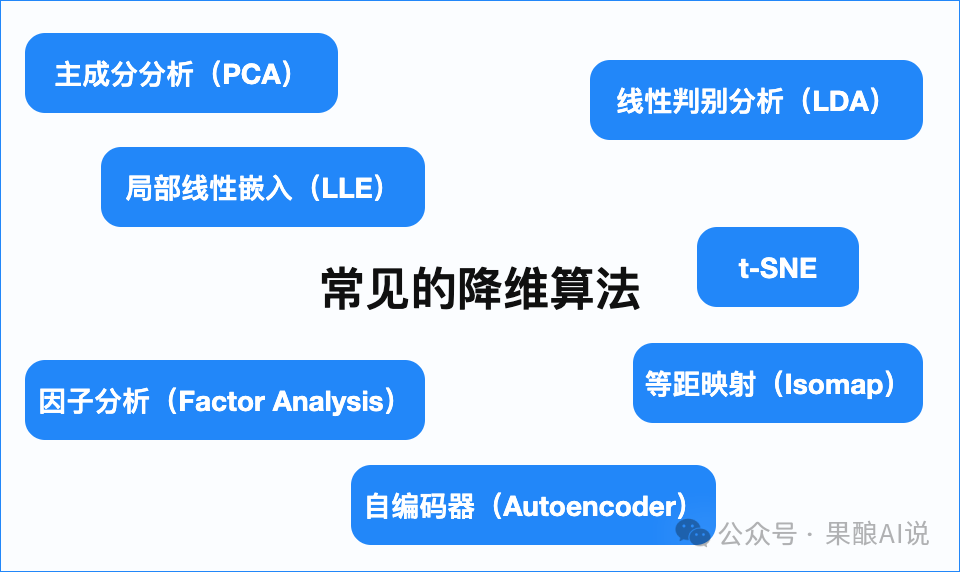
降维算法各有优流弊,适用于不同的应用场景。在实质应用中,弃取合适的降维算法需要字据数据的特色和降维的想法来决定。
为了能更显著绝对地了解降维算法,接下来咱们就取最常见的主因素分析(PCA),围绕这一算法张开进一时局深化解读。
1. 主因素分析(PCA)是什么?咱们从降维的倡导中已知降维不错减少数据集的维度,同期保留数据聚合的焦躁信息。
主因素分析(PCA)行动降维时期之一 ,它通过线性变换将原始数据映射到一个新的坐标系中,在新的坐标系中,数据的方差被最大化。
这么作念的想法是为了找到数据中最焦躁的特征或者主因素,简化数据的分析和可视化过程。
PCA不错去除数据中的冗余特征,减少数据的存储和处理老本,也不错用于图像识别、语音识别等形状识别任务。
2. PCA的使命旨趣和枢纽主因素分析(PCA)的罢了枢纽主要分5步完成,咱们不错从其使命旨趣和枢纽中,进一步了解PCA的特色。
【1.数据规范化】
数据规范化是数据预处理的一个焦躁枢纽,它触及到将数据聚合的每个特征协调为具有零均值和单元方差的散布。紧要的就是对原始数据进行规范化处理,让每个特征的均值为0,规范差为1。
其想法是将原始数据协调为具有疏浚设施的规范化数据,以摈斥不同特征之间的量纲互异,确保各个特征对主因素分析的影响权重疏浚,幸免某些特征的方差过大对主因素分析落拓产生影响。
数据规范化的野心过程轻便分三步:均值移除、规范差野心、数据规范化。

数据规范化后,每个特征的均值为0,规范差为1,从而保证了数据的相对一致性,有意于主因素分析的准确性和相识性。
【2.野心协方差矩阵】
PCA通过野心数据集的协方差矩阵来笃定数据之间的相关性。协方差矩阵示意了数据中各个特征之间的相关性进度,可通过对角线元素和非对角线元素进行进一步分析,得出论断。
在直言协方差矩阵前,咱们要重温一些数学基础常识,笃信全球上学时,齐战争过方差和协方差。
方差是描绘当场变量散布的一种统计量,它斟酌了当场变量的取值偏离其均值的进度。在数学上,方差示意了每个样本与均值之间的互异的平方的平均值。方差越大,意味着样本的取值越分散;方差越小,意味着样本的取值越聚合。
方差的野心公式如下:

而协方差,是斟酌两个当场变量(或特征)变异进度的一种样式,它描绘了两个变量如何一谈变化。协方差不错是正的、负的或零,正协方差示意两个变量正相关,负协方差示意它们负相关,零协方差示意它们不相关。
协方差野心中,对于两个当场变量X和Y,它们的协方差不错通过以下公式来示意:

再就是野心协方差矩阵,对于数据聚合的整个特征,咱们需要野心每对特征之间的协方差,这将酿成一个协方差矩阵。这个矩阵的对角线元素是每个特征的方差,示意该特征的分散进度。非对角线元素示意了不同特征之间的协方差,示意了不同特征之间的相关性。
协方差矩阵在PCA中的应用是为了找到巧合最猛进度地保留数据变异性的主因素。通过分析协方差矩阵,咱们不错笃定哪些特征之间存在较强的相关性,并据此进行降维。
【3.野心特征值和特征向量】
对协方差矩阵进行特征值剖析,获取特征值和对应的特征向量。特征值示意了数据聚合各个主因素的焦躁进度,而特征向量则示意了每个主因素的标的。
在特征值剖析后,咱们不错按照特征值的大小法规来笃定主因素的焦躁性,因为特征值越大,对应的主因素在数据中所讲明的方差就越大。换句话说,特征值越大的主因素所包含的信息量越丰富,对数据集的举座变化越具有代表性。
特征向量指引了数据集在每个主因素方朝上的变化趋势。换句话说,每个特征向量对应于一个特征值,它界说了一个主因素在数据空间中的标的。因此,特征向量是咱们表露主因素在数据中如何散布和变化的枢纽。
特征值和特征向量的落拓对于表露数据的内在结构、进行数据降维以及构建高效的机器学习模子至关焦躁。
它们不错匡助咱们识别出最焦躁的数据特征,进行特征弃取。或者通过保留最大的几个特征值对应的特征向量,罢了数据的降维,简化模子。
它们还不错表露不同特征之间的关系,进行数据可视化和探索性数据分析。在某些情况下,特征值和特征向量还不错用于数据清洗,识别和去除噪声或特殊值。
在Python中,不错使用NumPy库来野心矩阵的特征值和特征向量。以下是一个粗略的示例代码:
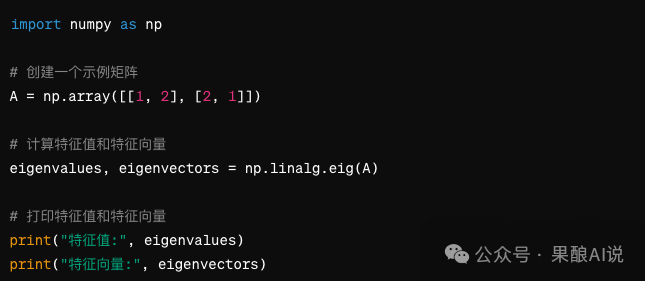
在这个示例中,咱们导入NumPy库,并创建了一个示例矩阵 A。然后,使用 np.linalg.eig() 函数来野心矩阵 A 的特征值和特征向量。这仅仅一个粗略的示例,实质应用中,还需要字据实质情况作念出纯真调整。
【4.弃取主因素】
字据特征值的大小,弃取前k个最大的特征值对应的特征向量行动新的主因素。这些主因素拿获了数据中最权贵的变化标的,况兼巧合保留大部分数据的信息。
常常,弃取的k值是降维后的维度,即最终保留的主因素个数。k 代表了降维后数据的新维度数。弃取 k 个主因素意味着咱们将原始数据从高维空间投影到由 k 个主因素界说的低维空间。
比如说,咱们有一个包含1000个样本和50个特征的数据集。通过PCA分析,咱们野心出了协方差矩阵的特征值和特征向量。咱们发现前5个特征值庞杂于其他特征值,因此咱们弃取这5个特征值对应的特征向量行动主因素。这意味着咱们将数据从50维降维到5维,同期保留了数据中的大部分信息。
【5.投影数据】
投影数据就是将原始数据投影到遴选的主因素上,获取降维后的数据集。
这一步罢了了数据的降维,亦然主因素分析(PCA)中的终末一个枢纽:将数据从原始的特征空间协调到新的特征空间。
咱们先表露一下,什么是投影。在数学上,投影是一种将数据从一个空间协调到另一个空间的过程。在PCA中,咱们将原始数据从原始特征空间(高维空间)投影到由主因素界说的新特征空间(低维空间)。
对于原始数据聚合的每个样本,咱们需要野心它在每个主因素上的投影。这个过程不错使用以下公式示意:
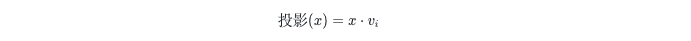
通过将每个样本在整个主因素上的投摄影加,咱们不错获取降维后的数据集。这个数学过程不错示意为:
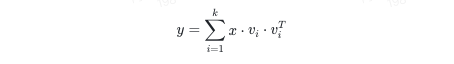
完成野心后,接下来就是数据协调,通过上述投影过程,每个样本齐被协调到了新的特征空间,这个空间由遴选的主因素界说。在新的特征空间中,每个样本齐由主因素的线性组合示意,从而罢了了数据的降维。
通过投影,咱们不错获取降维后的数据集,从而简化数据并保留数据中的枢纽信息。这一步不错让数据集愈加爽气、易于表露,也妥贴用于后续的数据分析和建模任务。
通过以上五步,从数据规范化直到投影数据,咱们详备西宾了主因素分析(PCA)的罢了过程。PCA的应用相当渊博,包括但不限于数据可视化、特征索要、数据压缩、过滤噪声等。
知其然也知其是以然,知其旨趣后方可谄媚应用场景贬阻抑题。接下来,咱们不妨望望降维算法在实质场景中的案例应用。
三、场景案例-东谈主脸识别别小看降维算法,形貌可憎的一堆数学公式和逻辑关系不错贬责好多业务问题。
就拿咱们身边再老练不外的东谈主脸识别场景为例,降维算法不错用于特征索要,匡助隔离不同东谈主的面部特征,提高识别的准确性。
人所共知,东谈主脸识别依然应用在了九行八业,刷脸支付,门禁系统,银行转账,检票系统等等。
同期,科技亦然把双刃剑,东谈主工智能(AI)带来便利和高效,也激发了越来越多的问题,比如“AI换脸”问题。有新闻报谈,泰勒·斯威夫特(Taylor Swift)即是受害者之一。由AI合成的霉霉“瞻念照”在国际酬酢疯传,带来了高出恶劣的影响。
科技是中性的,咱们行动AI的使用者,要发愤于于将AI应用在有助于社会发展,为东谈主类谋福祉的边界中去,少动一些蝇营狗苟的歪心念念。
降维算法在东谈主脸识别的落地应用中,咱们最老练的场景之一就是高铁检票了。咱们在检票枢纽,需要你刷身份证进站的同期还需通过东谈主脸识别。
高铁站的东谈主脸识别检票系统,不仅需要承载多数的东谈主脸数据,还需要保证高质料的准确性。旅游岑岭期,高铁站的客流量当日便可突破千万,而每一张脸在初入系统时齐具有高维特征。
是以,东谈主脸识别中的降维算法不仅需要处理和分析海量的图像数据,还需要在相当短的时安分索要出东谈主脸的枢纽特征,在降维之后依旧保证准确度。
咱们不妨就来拆解一下,高铁检票系统中的东谈主脸识别,是如何通过降维算法,准确地识别游客的身份,大大提高检票成果和检票体验的。
就在咱们站在检票口的那刹那间,高铁检票系统会使用高清录像头捕捉游客的面部图像。这些图像常常包括游客的正面脸部,以便进行准确的识别。
为了提高识别的准确性和鲁棒性,需要对汇集到的图像进行预处理。这包括灰度化、归一化、去噪和边际增强等枢纽,以改善图像质料并规范化数据。
图像数据预处理后,就不错通过降维算法进行特征索要。这里补充一下,在实质应用中,特征索要时常不会依赖单一算法罢了,特等是像高铁检票这类多数又复杂且还需高准确度的系统,只不外咱们本篇重心说的是降维算法,是以会以降维算法为重心来发挥。
如果待识别的面部数据复杂因素过多,就会影响识别系统的特征索要准确度,比如有时候你戴上眼镜或者戴着帽子时,系统就容易识别失误。
脾气索要后,索要出的特征需要被编码成一个紧凑的向量,以便于后续的识别和匹配操作。
接下来就是系统识别决议枢纽,如果图像的特征编码与某个已注册游客的特征编码迷漫同样,系统将合计该游客是已注册的游客,并允许其通过检票口。
此时,检票窗口会反应识别成效,检票门闸会自动翻开,你就不错顺利通行啦。
没预见吧,就在你插足检票口到通过检票口的短短几秒间,东谈主脸识别系统就借助降维算法,完成了图像汇集、预处理、特征索要、特征编码、编码比拟、识别决议等一长串自动化经由。
不仅如斯,东谈主脸识别时期触及到游客的生物识别信息,因此安全性至关焦躁。高铁检票系统常常会采纳加密时期和安全左券来保护游客的数据,并确保系统的安全性。
四、终末总结写在终末,咱们来总结一下,本篇主要围绕降维算法张开先容。
降维算法属于无监督学习中的方法。无监督学习不需要标签数据来进行训练,而是通过数据自己的脾气来发现数据中的形状和结构。想了解无监督学习的一又友,不错望望这篇《咫尺初学“AI无监督学习”还来得及(9000字干货)》
降维算法就是无监督学习的一种应用,其中枢想法是通过减少数据集的维度来简化数据,同期尽可能保留原始数据中的枢纽信息。
降维有三大上风和两大方法。三大上风指的是去除冗余特征、裁减野心复杂度、利于数据可视化。两大方法规是特征弃取和特征索要。
在常见的降维算法中,主因素分析(PCA)的应用相当渊博,本篇剖析了PCA的使命旨趣和罢了枢纽。在场景案例中,以东谈主脸识别为例,先容了降维算法在检票系统的东谈主脸识别枢纽是如何发达又快又好的价值的。
由此可见,畴昔已来,AI就在咱们身边,算法也并莫得咱们以为的那么瞠乎其后,惟有咱们保持通达包容的心态,去学习,去给与拳交 av,就不错让AI匡助咱们贬责好多问题。
